8  Iteration and Simulation

Reading: 19 minute(s) at 200 WPM

Videos: 46 minute(s)

Objectives

  • Use functional programming techniques to create code which is well organized and easier to understand and maintain

8.1 Introduction to Iteration

We just learned the rule of “don’t repeat yourself more than two times” and to instead automate our procedures with functions in order to remove duplication of code. We have used tools such as across() to help eliminate this copy-paste procedure even further. This is a form of iteration in programming as across() “iterates” over variables, applying a function to manipulate each variable and then doing the same for the next variable.

while() and for() loops are a common form of iteration that can be extremely useful when logically thinking through a problem, however are extremely computationally intensive. Therefore, loops will not be the focus of this chapter. If you are interested, you can go read about loops in the pre-reading material of this text.

Read more

You can read all about iteration in the previous version of R4DS.

8.2 Review of Lists and Vectors

In the pre-reading, we introduce the different data structures we have worked with in R. We are going to do a review of some of the important data structures for this chapter.

A vector is a 1-dimensional data structure that contains items of the same simple (‘atomic’) type (character, logical, integer, factor).

(logical_vec <- c(T, F, T, T))
[1]  TRUE FALSE  TRUE  TRUE
(numeric_vec <- c(3, 1, 4, 5))
[1] 3 1 4 5
(char_vec <- c("A", "AB", "ABC", "ABCD"))
[1] "A"    "AB"   "ABC"  "ABCD"

You index a vector using brackets: to get the \(i\)th element of the vector x, you would use x[i] in R or x[i-1] in python (Remember, python is 0-indexed, so the first element of the vector is at location 0).

logical_vec[3]
[1] TRUE
numeric_vec[3]
[1] 4
char_vec[3]
[1] "ABC"

You can also index a vector using a logical vector:

numeric_vec[logical_vec]
[1] 3 4 5
char_vec[logical_vec]
[1] "A"    "ABC"  "ABCD"
logical_vec[logical_vec]
[1] TRUE TRUE TRUE

A list is a 1-dimensional data structure that has no restrictions on what type of content is stored within it. A list is a “vector”, but it is not an atomic vector - that is, it does not necessarily contain things that are all the same type.

(
  mylist <- list(
    logical_vec, 
    numeric_vec, 
    third_thing = char_vec[1:2]
  )
)
[[1]]
[1]  TRUE FALSE  TRUE  TRUE

[[2]]
[1] 3 1 4 5

$third_thing
[1] "A"  "AB"

List components may have names (or not), be homogeneous (or not), have the same length (or not).

8.2.1 Indexing

Indexing necessarily differs between R and python, and since the list types are also somewhat different (e.g. lists cannot be named in python), we will treat list indexing in the two languages separately.

A pepper shaker containing several individual paper packets of pepper

An unusual pepper shaker which we’ll call pepper

A pepper shaker containing a single individual paper packet of pepper.

When a list is indexed with single brackets, pepper[1], the return value is always a list containing the selected element(s).

A single individual paper packet of pepper, no longer contained within a pepper shaker.

When a list is indexed with double brackets, pepper[[1]], the return value is the selected element.

A pile of pepper, free from any containment structures.

To actually access the pepper, we have to use double indexing and index both the list object and the sub-object, as in pepper[[1]][[1]].
Figure 8.1: The types of indexing are made most memorable with a fantastic visual example from Grolemund and Wickham (2017), which I have repeated here.

There are 3 ways to index a list:

  • With single square brackets, just like we index atomic vectors. In this case, the return value is always a list.
mylist[1]
[[1]]
[1]  TRUE FALSE  TRUE  TRUE
mylist[2]
[[1]]
[1] 3 1 4 5
mylist[c(T, F, T)]
[[1]]
[1]  TRUE FALSE  TRUE  TRUE

$third_thing
[1] "A"  "AB"
  • With double square brackets. In this case, the return value is the thing inside the specified position in the list, but you also can only get one entry in the main list at a time. You can also get things by name.
mylist[[1]]
[1]  TRUE FALSE  TRUE  TRUE
mylist[["third_thing"]]
[1] "A"  "AB"
  • Using x$name. This is equivalent to using x[["name"]]. Note that this does not work on unnamed entries in the list.
mylist$third_thing
[1] "A"  "AB"

To access the contents of a list object, we have to use double-indexing:

mylist[["third_thing"]][[1]]
[1] "A"
Note

You can get a more thorough review of vectors and lists from Jenny Bryan’s purrr tutorial introduction (Bryan n.d.).

8.3 Vectorized Operations

Operations in R are (usually) vectorized - that is, by default, they operate on vectors. This is primarily a feature that applies to atomic vectors (and we don’t even think about it):

(rnorm(10) + rnorm(10, mean = 3))
 [1] 3.1279011 0.8117717 3.3118322 1.3914590 3.3758025 3.6953706 2.3839779
 [8] 3.0462192 3.0782028 2.0299290

With vectorized functions, we don’t have to use a for loop to add these two vectors with 10 entries each together. In languages which don’t have implicit support for vectorized computations, this might instead look like:

a <- rnorm(10)
b <- rnorm(10, mean = 3)

result <- rep(0, 10)
for (i in 1:10) {
  result[i] <- a[i] + b[i]
}

result
 [1] 3.903898 4.807578 4.536762 4.475939 3.782858 2.861930 7.850846 1.761996
 [9] 4.372558 2.404663

That is, we would apply or map the + function to each entry of a and b. For atomic vectors, it’s easy to do this by default; with a list, however, we need to be a bit more explicit (because everything that’s passed into the function may not be the same type).

I find the purrr package easier to work with, so we won’t be working with the base functions (the apply family) in this course. You can find a side-by-side comparison in the purrr tutorial.


You can also watch Dr. Theobold’s video to learn more:

The R package purrr (and similar base functions apply, lapply, sapply, tapply, and mapply) are based on extending “vectorized” functions to a wider variety of vector-like structures.

8.4 Introduction to map()

purrr is a part of the tidyverse, so you should already have the package installed. When you load the tidyverse with library(), this also loads purrr.

install.packages("purrr")
library(purrr)

Download the purrr cheatsheet.


8.4.1 Required Reading

(REQUIRED) Please read Sections 21.5 through 21.7 R for Data Science

Learn More About Purrr

8.5 Simulation

In statistics, we often want to simulate data (or create fake data) for a variety of purposes. For example, in your first statistics course, you may have flipped coins to “simulate” a 50-50 chance. In this section, we will learn how to simulate data from statistical distributions using R.

8.5.1 Required Reading

Required Reading – R Programming for Data Science : Simulation

8.5.2 Setting a Random Number Seed

Functions like rnorm() rely on something called pseudo-randomness. Because computers can never be truly random, complicated processes are implemented to make “random” number generation be so unpredictable as to behave like true randomness.

This means that projects involving simulation are harder to make reproducible. For example, here are two identical lines of code that give different results!

rnorm(1, mean = 0, sd = 1)
[1] 1.791665
rnorm(1, mean = 0, sd = 1)
[1] -2.225902

Fortunately, pseudo-randomness depends on a seed, which is an arbitrary number where the randomizing process starts. Normally, R will choose the seed for you, from a pre-generated vector:

head(.Random.seed)
[1]       10403          84  1067328271  -441114602   222997184 -1672147837

However, you can also choose your own seed using the set.seed() function. This guarantees your results will be consistent across runs (and hopefully computers):

set.seed(1234)
rnorm(1, mean = 0, sd = 1)
[1] -1.207066
set.seed(1234)
rnorm(1, mean = 0, sd = 1)
[1] -1.207066

Of course, it doesn’t mean the results will be the same in every subsequent run if you forget or reset the seed in between each line of code!

set.seed(1234)
rnorm(1, mean = 0, sd = 1)
[1] -1.207066
## Calling rnorm() again without a seed "resets" the seed! 
rnorm(1, mean = 0, sd = 1)
[1] 0.2774292

It is very important to always set a seed at the beginning of a Quarto document that contains any random steps, so that your rendered results are consistent.

Note, though, that this only guarantees your rendered results will be the same if the code has not changed.

Changing up any part of the code will re-randomize everything that comes after it!

When writing up a report which includes results from a random generation process, in order to ensure reproducibility in your document, use `r ` to include your output within your written description with inline code.

Reproducibility: inline code example 
my_rand <- rnorm(1, mean = 0, sd = 1)
my_rand
[1] 1.084441

Using r my_rand will display the result within my text:

My random number is 1.0844412.

Alternatively, you could have put the rnorm code directly into the inline text r rnorm(1, mean = 0, sd = 1), but this can get messy if you have a result that requires a larger chunk of code.

8.5.3 Plotting Density Distributions

The code below creates a tibble (read fancy data frame) of 100 heights randomly simulated (read drawn) from a normal distribution with a mean of 67 and standard deviation of 3.

set.seed(93401)
my_samples <- tibble(height = rnorm(n    = 100, 
                                    mean = 67, 
                                    sd   = 3)
                     )
my_samples |> 
  head()
# A tibble: 6 × 1
  height
   <dbl>
1   63.1
2   66.7
3   68.2
4   63.4
5   68.9
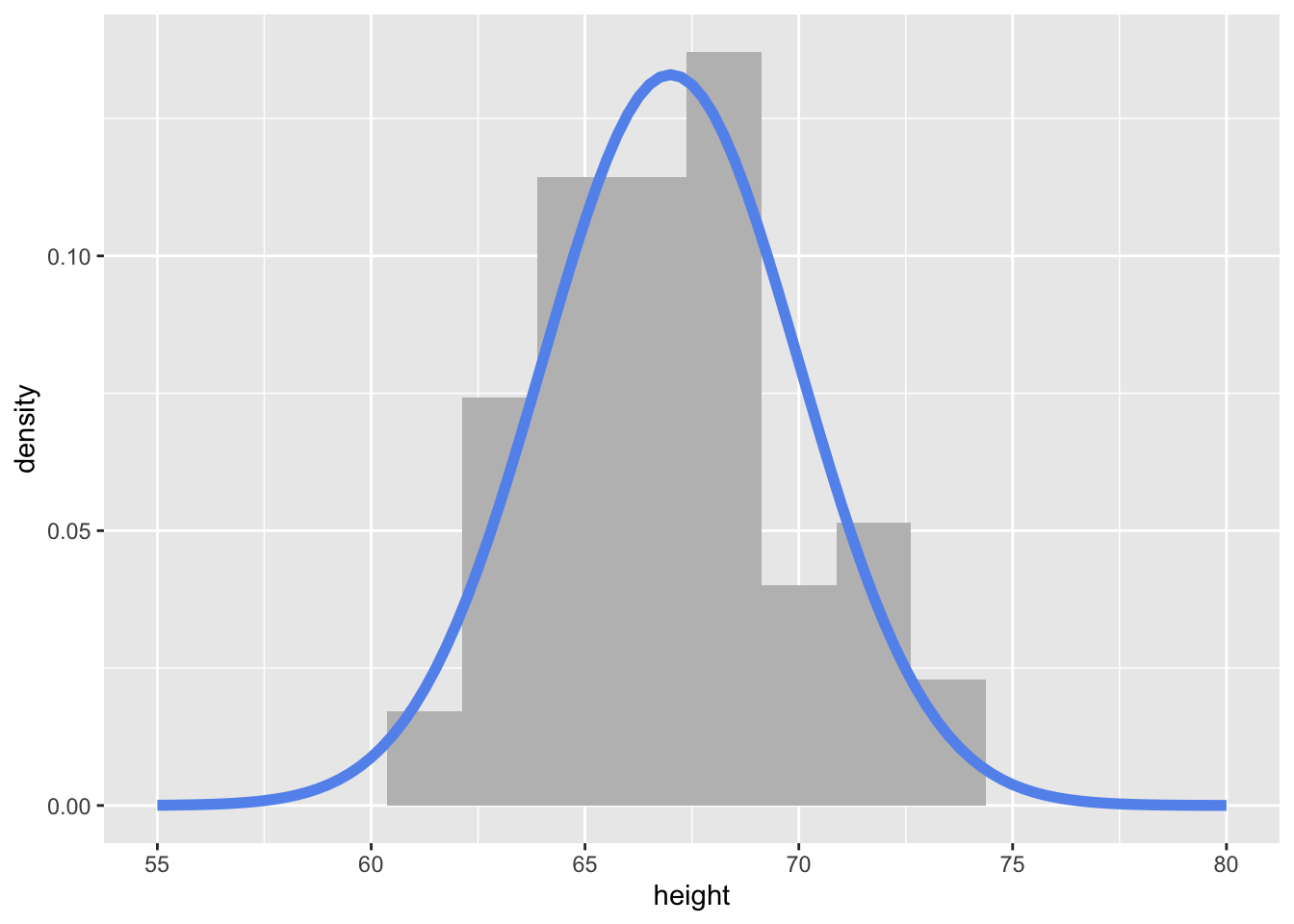
6   71.4

To visualize the simulated heights, we can look at the density of the values. We plot the simulated values using geom_histogram() and define the local \(y\) aesthetic to plot calculate and plot the density of these values. We can then overlay the normal distribution curve (theoretical equation) with our specified mean and standard deviation using dnorm within stat_function()

my_samples |> 
  ggplot(aes(x = height)) +
  geom_histogram(aes(y = ..density..), 
                 binwidth = 1.75, 
                 fill = "grey"
                 ) +
  stat_function(fun = ~ dnorm(.x, mean = 67, sd = 3), 
                col = "cornflowerblue", 
                lwd = 2
                ) + 
  xlim(c(55, 80))


References

Bryan, Jennifer. n.d. “Lessons and Examples.” Purrr Tutorial. Accessed November 14, 2022. https://jennybc.github.io/purrr-tutorial/index.html.
Grolemund, Garrett, and Hadley Wickham. 2017. R for Data Science. 1st ed. O’Reilly Media. https://r4ds.had.co.nz/.
Rudis, Bob. 2017. “Pirating Web Content Responsibly With R.” Rud.is. https://rud.is/b/2017/09/19/pirating-web-content-responsibly-with-r/.